Upon reflection on my free inquiry project, I can’t help but notice how far I’ve strayed. I started with an unassuming book, Power of Habit by Charles Duhigg, and ran wild with the subject matter. My earlier posts are more focused on the content of the book but my more recent posts have showcased what the implementation of that content allowed me to achieve. For information on how habit intersects with willpower and education, please check out this post from earlier. Otherwise, please enjoy the conclusion of my November foray into code.
Coding Recap
If you’ve been following this journey, you may already know what I’ve been looking to achieve. Visualizing the modulation of functions was a sticking point for me in pre-calculus. I noticed some of the students that I tutor have a similar issue. I am not aware of a resource that visualizes it in the way I would like, so I’ve resorted to learning how to do it myself with Python using an open-source library called Manim. This has been daunting, as coding is not something I’ve succeeded with in the past. However, I have managed to reduce the required willpower thanks to tricks I learned in Power of Habit, and progress has been rapid. In my efforts to animate the modulation of a function, I stumbled across solutions that were band-aids to the problem I was facing. I wasn’t technically modulating a function, I was just replacing one function with another and employing a fancy transition.
Solution! But further yet to go…
Updaters are the key! Notice the blue text “.add_updater” and the “get_value”. See the top-most examples and how “parabola.add.updater” had a function inside of it, indicated by “ax.plot”. This alteration of the “parabola” function defined just one line above has something special. “a.get_value()” allows me to insert a variable into the function, and determine the range and speed with which it modulates. This is an incredibly exciting mechanic, and it was a significant struggle getting it to work. I tried incorporating it into a visible math statement of the function, but I haven’t figured out how to display a defined element like “a_number” with “MathTex”. Instead, I slapped on a band-aid for now. Notice “text2=MathTex(“a=”)” and that it is set “.next_to(a_number” and shifted to the left twice. This manages to at least indicate that the variable, in this case, “a”, is the element modulating the function. I really hope to improve at this… This mechanic is certainly the key to everything. Once I learn to run multiple updates at once, all set into visible math statements, I will be able to start crafting animations more tailored to my struggling students. Please enjoy this pivotal render.
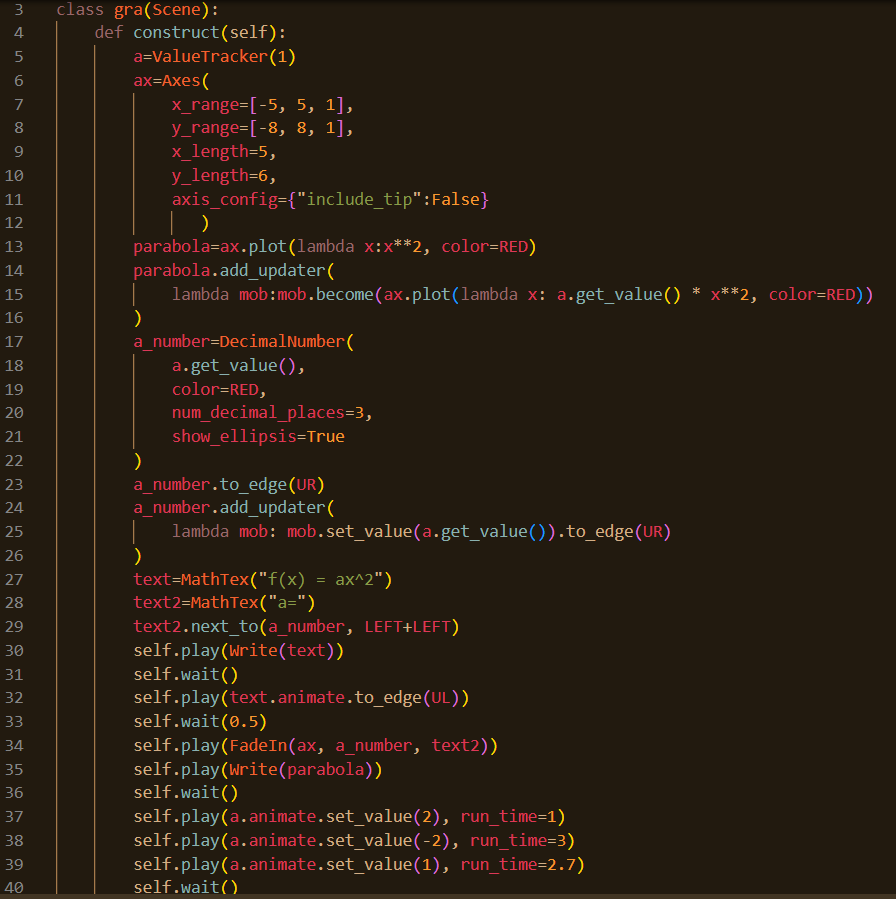
I know it’s no sine function, but this is the exact mechanism I’ve been looking for. It will take a while for me to use it efficiently, but I look forward to working on this tirelessly over the December break. I may even return to update (lol) any readers on my progress. If you’re interested, please leave a comment and let me know. Until then…
This is Jake… Signing off.
“Happiness is the feeling that power increases — that resistance is being overcome.“
–Friedrich Nietzsche
